Cela fait quelques années que la technologie existe, mais en 2010, le tableau blanc interactif (TBI) a connu un boom significatif. Il est en effet en passe de remplacer les tableaux verts (ou noirs) pour de nombreuses activités dans un grand nombre de classes : plus de 20% dans plusieurs pays, dont la France, et même plus de 90% en Grande-Bretagne. Cela est dû à un coût beaucoup plus abordable bien sûr mais aussi parce que cet outil apporte une réelle valeur ajoutée pédagogique.
Le TBI, c’est un écran de grande taille tactile. On peut se servir de ses doigts ou d’un stylet.
Voici quelques pistes pour évaluer l’apport d’un TBI. Certaines activités sont tout à fait réalisables avec un ordinateur couplé à un vidéo-projecteur mais parfois avec des efforts importants, alors qu’avec le TBI, cela devient naturel.
-En mathématiques, plusieurs activités bénéficient d’un apport important grâce
à cet outil :
1) Activités mentales.
C’est un support ludique et attractif auprès des élèves.
On bénéficie de fonctionnalités spécifiques (timing, insertions de figures, affichage de 2 questions en parallèle…).
2) Obtenir des résultats immédiatement avec une présentation soignée.
-Cela permet une correction dynamique d’exercices :
.Avec une validation instantanée des réponses.
.Avec des calculs répétitifs simplifiés.
-On peut mettre en place une adaptation rapide à l’exercice, qui peut être modifié en temps réel.
-Cela permet d’obtenir des tracé de figures :
.De la création jusqu’à une correction rapide.
.Et même une simplification de figures complexes.
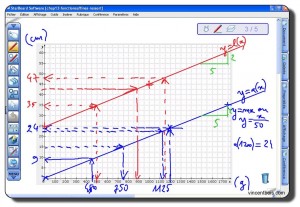
-On peut aussi créer des tableaux, des graphiques :
.Ce qui donne une correction claire et rapide.
.Les paramètres sont modifiables pour un prolongement de l’activité.
.Et cela aide à l’assimilation de l’outil Tableur, qui est un point du programme.
3) Animations dynamiques de type soutien visuel.
-On peut montrer des méthodes de tracé, comme la construction d’un triangle, ou encore le symétrique d’un point.
-On peut travailler sur l’influence de paramètres variables, comme le coefficient directeur d’une fonction affine.
-On peut aussi, d’une façon dynamique et soignée donner des rappels de cours, en particulier en géométrie.
Les tracés peuvent tourner en boucle, l’élève s’y référant selon ses besoins et le professeur dispose de plus de temps pour les élèves qui en ont le plus besoin.
D’une façon générale, cela aide à la création d’images mentales.
4) Mieux percevoir l’espace.
On obtient grâce à des logiciels spécifiques de géométrie dynamique dans l’espace une meilleure appropriation des représentations en perspective.
On construit des images mentales relatives à des situations de parallélisme et d’orthogonalité.
Les élèves ont une visualisation immédiate grâce à l’animation des figures.
Là aussi, on peut varier aisément les paramètres.
Toutefois, les élèves devront toujours continuer à :
• manipuler des solides en bois, en plastique …
• tracer des patrons, construire des solides.
5) Découvrir.
-Que dessiner n’est pas construire, que mesurer n’est pas prouver.
-Une nouvelle notion, une activité plus dynamique, ou simplement une mise en commun des résultats des élèves.
6) Modéliser la situation.
On peut faire une représentation des données du problème, en particulier dans des cas qui peuvent paraître complexes pour les élèves.
7) Explorer une situation problème (toutefois de façon plus efficace en salle informatique qu’avec le TBI).
Les logiciels de géométrie dynamique et les tableurs sont des outils de recherche.
Ils permettent à l’élève :
-d’expérimenter : tâtonner, observer, explorer, tester, ajouter des contraintes, revenir en arrière,
-d’émettre des conjectures,
-de trouver des pistes pour démontrer.
Le logiciel est un outil pour l’aide à la résolution.
C’est un plus par rapport au papier et au crayon qui reste le moyen de recherche indispensable pour résoudre un problème.